工程師學習MInitab軟體

很多人擁有Minitab軟體，但如何快速有效率學好並運用Minitab是網站上很多人討論的，今天偶然逛到Minitab官方網站，看到2011年在美國本土針對製造業人員做Minitab五天訓練課程，我想這是Minitab官方對製造業從業人員訓練內容的主流觀點看法，值得自學者參考方向

Minitab pk JMP – 01 制作特性要因图 – 4 Quality Companion插花教程

Quality Companion是Minitab公司協助達成Six Sigma品質改善的輔助Minitab的工具軟體，因此可以利用Quality Companion製作魚骨圖

[DOE DIY ]01 學DOE自己來 - DOE基本概念-6試驗設計解析(3組)

情境：兄妹三人比賽後已有成績(3人的比賽) 

1 兄妹共三人比賽結果成績記錄如下表

[DOE DIY ]01 學DOE自己來 - DOE基本概念-5試驗設計解析(2組)

情境：兄弟二人比賽後已有成績(2人的比賽)

Minitab pk JMP – 01 製作特性要因圖 – 3 Visio插花教程

筆者十多年來製作魚骨圖並不用Minitab或JMP，而是用微軟的Visio 2000到2003，使用起來方便很多，Visio畫魚骨圖的概念如下圖

Minitab 的 power and sample size計數值應用例

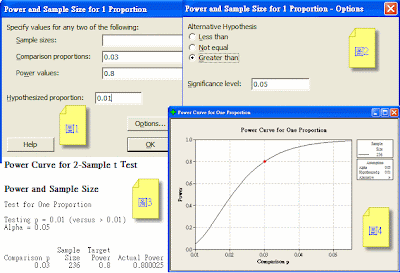
1 1P單比例(Proportion)計數值例

目前某製程不良率是1%，若第1種錯誤希望控制在0.05，並希望不良率若達3%(或以上)時能有80%被檢出，試問樣本數應取多少

檢驗的假設 H₀: P= 0.01   H₁: > 0.01
Minitab操作從功能表 Stat > Power and Sample Size > 1 Proportions
                                     統計 > 檢出力和樣本數量 > 1P單比例
操作步驟：圖1與圖2確定後Minitab計算結果於會話視窗與曲線圖如圖3~4

結論：若希望得到0.9檢出力則樣本數量是4191，又若希望得到0.8檢出力則樣本數量是3026。


2 2P雙比率計數值例
若製程有二條生產線且生產線2的不良率是12%，若第1種錯誤希望控制在0.05，而希望當生產線1不良率優於生產線2達2%以上(亦即P2-P1 > 2% )時有80%與90%被檢出，試問樣本數應取多少

檢驗的假設 H₀: P₁=P₂   H₁: P₁
Minitab功能表 Stat > Power and Sample Size > 2 Proportions
                         統計 > 檢出力和樣本數量 > 2P雙比例

操作步驟：圖1與圖2確定後Minitab計算結果於會話視窗與曲線圖如圖3~4

結論：若希望得到0.8檢出力則樣本數量是236。

Minitab 的 power and sample size計量值應用例

1 單樣本 z 的檢出力和樣本數量
若要生產重量為 250±3gm 的產品，已知製程服從常態分佈，且標準差已知為10gm，若第I種錯誤希望控制在0.05，而希望制程平均差異高於3gm時有80%機會被檢定出有顯著性，試問應取多少樣本數。

應用Minitab 統計 > 檢出力和樣本數量 > 1z 單樣本 z,
   差值：3
   檢出力值：0.8
   標準差：10
   選項按鈕默認 備擇假設 - 不等於
                             顯著性水準 - 0.05

輸出結果
Power and Sample Size
1-Sample Z Test
      Testing mean = null (versus not = null)
      Calculating power for mean = null + difference
      Alpha = 0.05  Assumed standard deviation = 10
                        Sample  Target
      Difference    Size    Power  Actual Power
                      3      88        0.8       0.803527

結論：應抽取88個來進行檢定，若差異值高於3gm時有80%機會為顯著性( (實際為0.803527)

2 單樣本 t 的檢出力和樣本數量
若要生產重量為 250±3gm 的產品，若第1種錯誤希望控制在0.05，而希望差異高於3gm時有80%被檢出，依據以往調查制程標準差為10gm

應用Minitab 統計 > 檢出力和樣本數量 > 1t 單樣本 t,
    差值：3
    檢出力值：0.8
    標準差：10
圖1是輸入，圖2是輸出結果得知樣本數量應為90，圖3是檢出力曲線

3 雙樣本 t 的檢出力和樣本數量
想知道A與B二個生產線產品的重量有所不同，實務作法是各自二生產線抽取n₁、n₂樣本，然後進行 t 檢定，其假設是 H0: μ₁ = μ₂，而對立假設可能選擇μ₁ > μ₂、μ₁ ≠ μ₂或μ₁ < μ₂。
在檢出力(Power)的研究中通常是假設n₁=n₂的，假若第1種錯誤希望控制在0.05，而希望差異高於3、1、0.5 gm時，有80%、90%被檢定出有顯著，依據以往調查製程標準差為2gm，樣本數應取多少

應用Minitab 統計 > 檢出力和樣本數量 > 2t 雙樣本 t,
   差值：3 1 0.5
   檢出力值：0.9 0.8
   標準差：2
   選項按鈕 > 不等於
                       顯著性水準 0.05

Minitab的檢出力與樣本數

1 何謂檢出力

若虛無假設(H₀)實際上是不成立，而在實施假設檢定中，能夠正確否定此項虛無假設的機率稱為檢出力(Power，Minitab簡體譯為功效)

活用Excel於品管統計與解析課程設計想法

1 課程設計目標：

多數企業的品管活動經過一段時間運作大多已經定型化，而適合以電腦來進行品管作業，而快速提供品管必要情報，以利品質的維持與改善。而作為品管運用的諸多電腦軟體中，微軟公司 Excel軟體因兼備資料庫、統計計算與繪圖功能等三大功能，且其運算資料的可視覺化與通俗化，是企業處理品管資料最廣泛採用與適用的，另外各企業辦公室也都有現成 Excel軟體而不必另外投資，所以在企業界普受歡迎。

本課程將導入品管統計與解析用 Excel的方法，期望企業員工活用而有效率的執行其品管業務，課程將以案例講解，學員於課後將獲得上課案例講解的 Excel檔案，方便課後複習與應用到現場實務工作。

2 課程內容：

一、運用微軟公司Excel於品管的重要特性

    1.統計量計算

    2.圖表製作

    3.統計分配計算與運用

    4.常態分配的運用

    5.圖表製作

    6.品管資料彙總與層別分析

二、用Excel作入廠品質檢驗(IQC)作法與實施案例

    1.Mil-Std-105E抽樣計劃

    2.Mil-Std-1916抽樣計劃

三、用Excel作製程品質管制(IPQC)作法與實施案例

    1.管制圖製作

    2.製程能力分析

    3.量測系統分析(MSA)

四、用Excel作出廠品質檢驗(FQC)作法與實施案例

    1.出貨品質評價分析

    2.抱怨處理與解析

    3.可靠度研究

五、用Excel作品質改善作法與實施案例

    1.QC七手法活用

    2.製程研究與解析

    3.量測系統分析(MSA)

    4.品質月報製作

用Excel作統計需要小心-3 使用四分位與百分位數

統計量中位數(median又稱中值)是將一群資料分為兩半，使50%的資料小於中位數，另50%資料大於中位數，相對於平均數，中位數的優點是對不受離群值(Outlier)的影響。

從中位數可延伸到四分位數(Quartile)，第一四分位數(Q1)是指25%資料小於Q1，75%資料大於Q1，依此類推第二~四四分位數(Q2~Q4)，其中Q2就是中位數，再從此處推展就是百分位數(p-th Percentile)，四分位數最常用來製作箱線圖(Boxplot)，而百分位元數用來製作常態分配機率圖是基本統計學上很重要的統計量，居於百分位與四分位數同質性，所以本文只談四位位數。

若使用Excel 函數來計算四分位元，則須注意只有2010的Quartile.exc與Minitab或JMP計算一致如下圖紅框的部分

數據例：x	1	2		3		4		5		6
Excel 計算
使用函數 Quart(第×分位數)			0		1		2		3		4
=Quartile(array,QUART)			1		2.25		3.5		4.75		6
=Quartile.exc(array,QUART)			#NUM!		1.75		3.50		5.25		#NUM!
=Quartile.inc(array,QUART)			1		2.25		3.50		4.75		6
其他統計軟體
Minitab > Basic statistics 計算			1		1.75		3.50		5.25		6
JMP > Distribution 計算			1		1.75		3.50		5.25		6

四分位數(Quartile)之第一四分位數(Q1)是指25%資料小於Q1，75%資料大於Q1，依此類推第二~四四分位數，四分位數最常用來製作箱線圖(Boxplot)，若使用Excel Quartile函數來計算四分位元數，則須注意只有2010的Quartile.exc與Minitab或JMP計算一致如下圖紅框的部分

用Excel作統計需要小心-2- 使用TINV函數老是出錯

Excel的機率函數中就屬T-分佈(Student's t-distribution)最難使用，儘管到Excel 2010還是老出錯，只怪自己沒有用心去閱讀函數的說明。

使用TINV的場合是，當要計算一組資料平均值的置信區間CI(Confidence interval)，就需要用到TINV函數，例如：一組樣本數n=10的資料，計算求出xbar(平均值)=10，s(標準差)=2，那麼要計算平均值的95%置信區間CI，則需要此公式

CI=xbar ± t(α/2) * s/√n

公式中t(α/2)是在自由度n-1，α=1-0.95=5%，雙尾t分佈的反函數，若查表應為2.262

若使用Excel t-分佈函數，到2010版有3個相關函數

1 TINV(p,df)：Execl各版本原有的函數，TINV傳回t-分佈的雙尾反函數，所以運用時以 tinv (2*α/2 = 0.05，9) = 2.262157，此處多麼與公式t(α/2)格格不入而出錯，因此，使用上雖提心吊膽但也老出錯

2 T.INV.2T(p,df)：2010版excel 傳回t-分佈的雙尾反函數，與TINV相同，所以仍然為t.inv.2t (2*α/2 = 0.05，9) = 2.262157

3 T.INV(p,df)：2010版excel 傳回t-分佈的左尾反函數，所以運用時以 t.inv (α/2 = 0.025，9) = -2.262157，因為左尾所以為負值。

T.INV似乎比較接近統計學的公式，所以日後需要TINV函數時，我會選擇T.INV才不會錯

Excel 2010、2013或2016檢查有無安裝『分析工具箱』的方法

Excel 2010、2013或2016通常已經安裝好『分析工具箱』，但是未經啟動，因此要使用『分析工具箱』必須先做啟動的動作

[DOE DIY ]01 學DOE自己來 - DOE基本概念-4 紙蜻蜓比賽試驗設計討論

情境：當兄弟二人各做一個紙蜻蜓要比賽誰的最好時，妹妹回來了吵著也要參加比賽，如何重新設計比賽(試驗)計畫 

Minitab pk JMP – 01 製作特性要因圖 – 2 JMP教程

特性要因圖又稱魚骨圖是QC七大手法之一，是協助發掘問題要因的工具，Minitab與JMP都提供繪製魚骨圖的功能

JMP繪製魚骨圖

1 JMP繪製魚骨圖有二個途徑

1) 透過數據表輸入要因資料後做成魚骨圖 – 進入JMP然後建立數據表後再繪製魚骨圖

2) 直接在預設魚骨圖上繪製編輯魚骨圖 – 進入JMP在沒有數據表的狀況下啟動繪製魚骨圖，出現預設魚骨圖畫面後可直接在圖上編輯修改內容，很適合一邊進行魚骨圖腦力激盪一邊直接記錄(但需要熟練)

2 透過數據表輸入要因資料後做成魚骨圖

1)  資料佈署

透過數據表輸入要因資料後做成魚骨圖的方法參考下圖共有3個步驟，JMP設計上的思維也是以”要因單元”來設計，如下圖圖1數據表上的” 父項”、”子項”二個欄數據表需給予”父項級要因”與”子項級子要因”的情報，如此才可以表示因子間的隸屬關係，與Minitab不同的是將”要因單元”全部放到2欄上，如此確實比Minitab工作表清爽得多，JMP不在意數據表上”要因單元”的順序，JMP會按父子邏輯自動排序

2) 繪製魚骨圖

啟用繪製魚骨圖路徑，JMP 9 [圖形(Graph)] > [關係圖(Diagram)]，JMP 8以前版本稱為因果圖(Cause-and-Effect)，出現圖2對話框，填入[Y，子項]與[X，父項]後按確定後即輸出圖3的魚骨圖，不過字體與顏色都是制式

3) 如需要進一步修飾魚骨圖

用滑鼠一到要因附近會出現”要因單元框”後，以滑鼠右鍵點[本文] > [顏色]或[字體]來編輯要因字體或顏色，也可直接添加或刪除圖內的要因，此點比Minita優異很多

3 直接在預設魚骨圖上繪製編輯魚骨圖

1) 呼叫關係圖(魚骨圖)

在沒有數據表存在下，啟用繪製魚骨圖路徑，JMP 9 [圖形(Graph)] > [關係圖(Diagram)]，JMP 8以前版本稱為因果圖(Cause-and-Effect)，如下圖圖1

2) 添加"人機料法他”5個大要因並刪除預設原因1、原因2

本例大要因為檢驗、銲劑過程、板材、元件、元件插入等5個項目，所以將圖1的預設魚骨圖內容改為如圖2，此處需要移動滑鼠到適當位置時便會啟動整個魚骨圖，並出現一個筆者稱之為『要因單元框』(如圖3的灰色框)，也可使用滑鼠移動到適當位置，以上的方法適用於魚骨圖中的所有大小要因的編輯方法。

編輯時需要運用到滑鼠右鍵快顯功能表中的插入與移動，在此舉一個例，想在大要因” 檢驗”下面添加2個要因，則將滑鼠移到大要因”檢驗”處，顯示”要因單元框”後，滑鼠右鍵點[插入] > [之下]，”之下”的意思表示插入的要因將為其小要因，在出現輸入框上填入”測試”、”測試覆蓋率”及 ”測試員”等三項，確定後即添加該3個子要因到”檢驗”下、為了美觀利用”移動”功能將子要因移到另一側

3) 如需要進一步修飾魚骨圖

如同透過數據表繪製魚骨圖一樣，可利用滑鼠右鍵快顯功能 [本文] > [顏色]或[字體]來編輯要因字體或顏色，或添加或刪除要因。

4 對JMP的評論

1) 因為可以直接在預設魚骨圖上繪製編輯魚骨圖，適合於腦力激盪會議上直接繪製魚骨圖

2) 可以對重要要因加以標示(如圈選、紅色或粗體字)

3) JMP除可做成魚骨圖外，還可繪製為階層圖或巢狀圖

4) JMP又可直接生成Script，方便將魚骨圖傳遞，而不必經由數據表重新製圖

Minitab pk JMP – 01 製作特性要因圖 – 1 Minitab教程

特性要因圖又稱魚骨圖是QC七大手法之一，是協助發掘問題要因的工具，Minitab與JMP都提供繪製魚骨圖的功能

[DOE DIY ]01 學DOE自己來 - DOE基本概念-3 紙蜻蜓比賽試驗設計

情境：兄弟二人各做一個紙蜻蜓要比賽誰的最好，本文探討如何設計比賽(試驗)計畫

[DOE DIY ]01 學DOE自己來 - DOE基本概念-2 紙蜻蜓比賽

情境：兄弟二人各做一個紙蜻蜓要比賽誰的最好，並請媽媽作裁判並幫忙計時

討論DOE三原理：

[DOE DIY ]01 學DOE自己來 - DOE基本概念

1. 學DOE還是要進行試驗，透過試驗設計與數據解析，才能體會DOE
2. DOE授課上有很多包含Catapult等數十種寓教於樂遊戲，其中最有名廣泛被運用的遊戲是紙蜻蜓，大師Box在其DOE教科書上提到紙蜻蜓的因子試驗設計，因為紙蜻蜓(Paper helicopter)很容易進行試驗是學習DOE的教材，下圖是紙蜻蜓簡單造型之一

實施DOE的背後知識-拋體射程研究為例2

續前文實施DOE的背後知識-拋體射程研究為例1後，本文將談運用DOE推導實驗式模型的過程與問題